生産量が20％増えるとリードタイムは何倍？｜スマートファクトリー事業・FAプロダクツ

直感とは異なるリードタイムの増減予測

人というのは、予測を立てるとき直線的、直感的になります。その直感は必ずしも現実と合致しないケースがあります。
製造業では20%の生産増になれば、リードタイムは20%増える。サービス業では20%の顧客増加は20%のサービス待ち時間の増加と予測します。
これは、稼働率や顧客の流入率が低い場合や初めから同期が取れている場合は間違ってはいません。しかし、現実の世界では、そのような場合の方が遥かに少ないといって良いでしょう。

待ち行列理論とは

待ち行列理論というものが古くからあります。
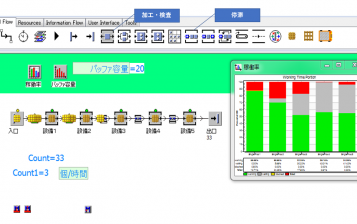
これは、顧客がサービスを受けるときの、混雑状況を、数理モデルを用いて解析する理論です。例えば、銀行の窓口がいくつあれば、顧客のサービスが適正に行われ、窓口で待たされずに済むのかという問題を解くのに利用されています。

身近な例では、ラーメン屋のカウンターの数を決めることがあります。市場調査の結果、単位時間当たり来客数を予測し、それに合わせてカウンター数を決めます。ここで、数が多すぎると店は狭くなるし、調理場も狭くなり、サービスの低下を招きやすくなります。それを避けるべく店舗面積を増やすとテナント料が増えます。コストが逼迫することになります。逆に数を減らすと顧客を待たせることになり、長時間の待ち時間によっては顧客を諦めて帰ります。機会損失の問題が発生します。

結果的には、顧客が諦めて帰ることのない程度にカウンターが埋まるように数を決めます。
店主は20%程度増えても、待ち時間が20%増えるなら顧客は待つであろうと予想を立てます。
しかし、この予測は取り返しのつかない結果を招くことがあります。。
顧客の流入数の増加と待ち時間の増加は一次関数で比例するのではないのです。

20%の負荷でリードタイムが倍に!!!

かつて、第二次世界大戦中に、アメリカからイギリスへ送られていた護送船団中80%はニューヨーク港から、残りの20%はボルチモア港から出港していました。海軍はそれぞれに対して護衛艦艇をつけることは不経済であると考え、全部をニューヨーク港から出すことに決定し、20%分をニューヨーク港へ吸収しました。しかし、所要時間が2倍になり護衛艦艇節約の効果が失われるという事態が発生しました。海軍当局は、サボタージュが始まったのではないかと原因を調査しましたが、そのような事実はなく、理由が不明でした。この問題をOR(Operation Research )グループのモース(P.M. Morse)教授が調べた結果、待ち行列の原理の通り20%のインプットの増加が待ち時間の2倍の増加になっていたのです。その後、再び20%をボルチモア港から出すことにしたら。元のように所要時間は半減したのであす。
☆種明かしをすると。。。
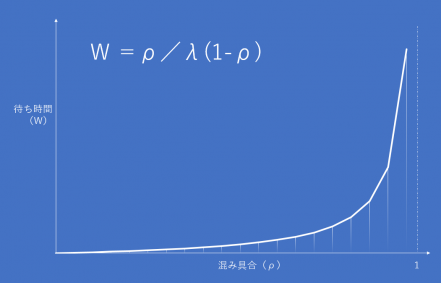
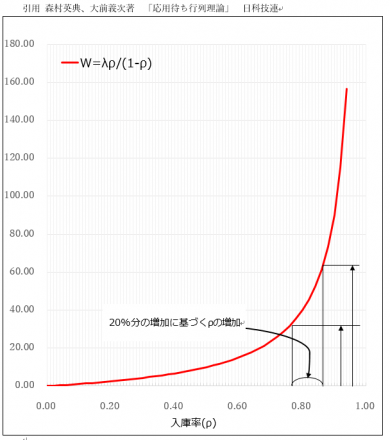
待ち行列の理論の基礎的な式は次の通りです。。

W = ρ / λ(1 -ρ)

W : 所要時間 (サービスを受けるまでの時間、待ち時間)
λ : 平均到着率(単位時間当たりの入庫数)
ρ　: 入庫率(平均サービス時間における平均到着数、混み具合)

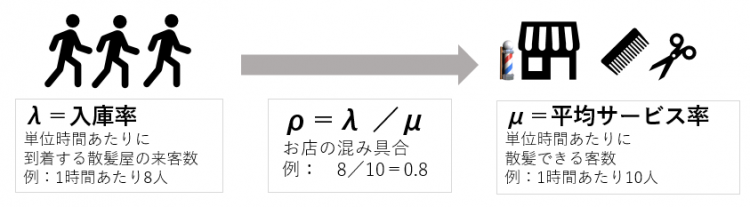
sanpatu2

ここでは式の成り立ちの説明は省略します。入庫率は簡単にいうと込み具合です。上記の散髪屋さんの例で説明すると、単位時間当たり10人散髪できるときに、単位時間当たりに8人が来客する場合、入庫率は0.8です。単位時間当たり10人の顧客が到着すると入庫率は1.0になります。常に塞がっているといことになります。そして1.0のときが、所要時間が無限に長くなるのは信じられないと思われますが、待ち行列理論では人や物がでたらめ(ランダム)に到着し、サービスは指数分布に従うという前提条件ではそうなるのです。ここではサービスを行うと同時に必ず顧客が到着するということは想定していません。そもそも、そのような取り決めのあるサービスでは問題が起きません。

どう対処すれば良いのか?

このような現象は、高速道路の料金所ゲートの渋滞など身近にも沢山あります。
また、生産ラインにおいて、ラインが少しでも複雑になるとライン全体で同期が取れるということはなくなります。なので生産量が20%増加するとリードタイムも2倍、3倍になるということも十分に起こります。納期回答で20%の生産増だから20%の納期遅れと予想したら大火傷をします。逆に20%の改善をすることで、リードタイムが劇的に短くなることもあります。

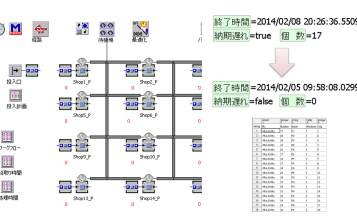
そこで生産ラインをコンピューター上でシミュレーションしてリードタイムを予測し、現場改善の効果を検証する価値というのは、古典的な待ち行列理論からも十分裏付けられます。複雑でなくても単純なモデルでも20%の増減は、明暗を分けるのです。
定量的に効果とリスクを把握して改善を計画的に行うことが一番の対処方法だと言えます。

引用森村英典、大前義次著　「応用待ち行列理論」　日科技連

waiting graph 3